In This Content
Introduction
Angles of elevation and depression are fundamental concepts in trigonometry and geometry that play a crucial role in various real-life scenarios. Understanding these angles is essential for solving problems related to heights, distances, and measurements. In this article, we will delve into what angles of elevation and depression are, how to calculate them, and explore practical applications of these concepts in different fields.
Table of Contents
- What are Angles of Elevation and Depression?
- How to Measure Angles of Elevation and Depression
- Calculating Angles of Elevation and Depression
- Applications in Architecture and Engineering
- Angles of Elevation and Depression in Physics
- Using Angles of Elevation in Astronomy
- Applying Angles of Depression in Geography
- Surveying and Mapping with Angles of Elevation and Depression
- Understanding Angles of Elevation in Sports
- Marine Navigation and Angles of Depression
- Mathematics and Trigonometry: Solving Elevation and Depression Problems
- Importance of Angles of Elevation and Depression in Photography
- Medical Applications: Angles of Elevation and Depression in Radiology
- Safety and Rescue Operations: Utilizing Angles of Elevation and Depression
- Conclusion
- FAQs
What are Angles of Elevation and Depression?
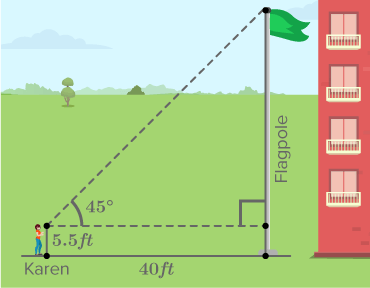
Angles of elevation and depression are types of angles formed between the line of sight and a horizontal line. When an observer looks upwards at an object, the angle formed between the line of sight and the horizontal line is called the angle of elevation. Conversely, when an observer looks downwards at an object, the angle formed between the line of sight and the horizontal line is called the angle of depression.
How to Measure Angles of Elevation and Depression
To measure angles of elevation and depression, you need two main components: the horizontal line and the line of sight. The horizontal line is a reference line parallel to the ground, while the line of sight is the line between the observer’s eye and the object being observed.
To measure the angle of elevation, extend the horizontal line from the observer to the object and draw a line of sight. The angle between these two lines is the angle of elevation.
To measure the angle of depression, extend the horizontal line from the observer to the object, but this time the line of sight will be directed downwards. The angle between the horizontal line and the line of sight is the angle of depression.
Calculating Angles of Elevation and Depression
The process of calculating angles of elevation and depression involves trigonometric functions such as sine, cosine, and tangent. By using these functions, along with known measurements such as distances and heights, we can determine the angles accurately.
For example, if the height of an object and the distance from the observer are known, the angle of elevation can be calculated using the tangent function. Similarly, in cases where the height of the observer and the distance to the object are known, the angle of depression can be calculated using the same trigonometric functions.
Applications in Architecture and Engineering
Angles of elevation and depression are extensively used in architecture and engineering for designing and constructing various structures. Architects use these angles to determine the best possible height and location for a building to optimize views and natural lighting.
Engineers utilize angles of elevation and depression when planning the slope of roads, railways, and ramps, ensuring smooth and safe transportation.
Angles of Elevation and Depression in Physics
In physics, these angles are crucial for analyzing projectile motion. When an object is launched into the air, the angle of elevation directly affects its trajectory and maximum range. Understanding these angles allows physicists to predict the motion of projectiles accurately.
Using Angles of Elevation in Astronomy
Astronomers rely on angles of elevation to observe celestial objects. Telescopes and observatories are positioned at specific angles to maximize their field of view and capture clear images of stars, planets, and other celestial bodies.
Applying Angles of Depression in Geography
Geographers use angles of depression to determine the height of mountains, buildings, or other objects in a landscape. By measuring the angle of depression to a known point, they can calculate the height of the object.
Surveying and Mapping with Angles of Elevation and Depression
Surveyors and cartographers use these angles for accurate mapping and land surveying. By measuring angles from different points, they can create detailed topographic maps and define property boundaries.
Understanding Angles of Elevation in Sports
Angles of elevation are essential in various sports, especially in sports like golf and basketball. Players need to calculate the angle at which they must launch the ball to achieve the desired trajectory and score points.
Marine Navigation and Angles of Depression
Marine navigators use angles of depression to determine the distance between a ship and a lighthouse or other landmarks. This information is crucial for safe navigation at sea.
Mathematics and Trigonometry: Solving Elevation and Depression Problems
In mathematics, angles of elevation and depression are used to solve trigonometric problems. By applying trigonometric ratios and principles, students can find missing side lengths or angles in triangles and other geometric shapes.
Importance of Angles of Elevation and Depression in Photography
Photographers use these angles to capture stunning shots from unique perspectives. By adjusting the angle of elevation or depression, photographers can create visually appealing and captivating images.
Medical Applications: Angles of Elevation and Depression in Radiology
In radiology, angles of elevation and depression play a role in positioning X-ray machines and obtaining clear images of specific body parts. Proper angles ensure accurate diagnoses and treatment plans.
Safety and Rescue Operations: Utilizing Angles of Elevation and Depression
Safety personnel and rescue teams use these angles to assess the height of buildings during emergency situations. This information helps them plan safe evacuation procedures and deploy resources effectively.
Conclusion
Angles of elevation and depression are versatile concepts with applications in various fields. From architecture and engineering to sports and photography, these angles provide valuable insights and solutions. Understanding how to measure and calculate these angles is essential for professionals and enthusiasts alike, enabling them to tackle real-world challenges with precision and accuracy.
FAQs
- What is the difference between the angle of elevation and the angle of depression?
- How do surveyors use angles of elevation and depression in their work?
- Can angles of elevation be negative?
- How do angles of elevation affect the range of a projectile?
- What role do angles of depression play in marine navigation?

