
Angles of elevation and depression are important concepts in geometry and trigonometry that are widely used in various fields such as engineering, architecture, and surveying. Understanding these angles is crucial for accurately measuring heights, distances, and angles in real-world applications. In this article, we will explore the fundamentals of angles of elevation and depression and provide practical examples to enhance your understanding. So, let’s dive in!
In This Content
1. Introduction
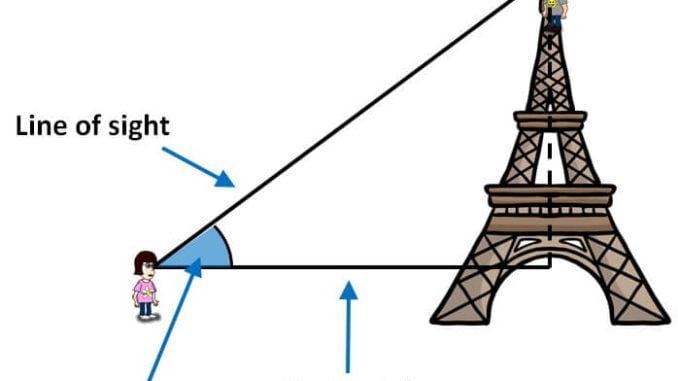
Angles of elevation and depression refer to the upward and downward angles formed between a horizontal line and the line of sight from an observer to an object. These angles are measured from the observer’s eye level or horizontal reference line.
2. Angles of Elevation
Angles of elevation occur when the line of sight is above the horizontal line or eye level. They are used to measure the height of an object or the angle required to look up at an object.
3. Examples of Angles of Elevation
- Calculating the height of a flagpole using the angle of elevation from the ground.
- Determining the angle at which a rocket launches into the sky.
- Measuring the height of a building by using the angle of elevation from a known distance.
4. Angles of Depression
Angles of depression, on the other hand, occur when the line of sight is below the horizontal line or eye level. They are used to measure the depth or the angle required to look down at an object.
5. Examples of Angles of Depression
- Determining the depth of a lake by measuring the angle of depression from a known height.
- Calculating the angle at which a diver descends below the water surface.
- Measuring the angle at which a plane is descending during landing.
6. Applications of Angles of Elevation and Depression
Angles of elevation and depression have numerous practical applications. Some common examples include:
- Surveying land and mapping topography.
- Designing ramps and inclined planes.
- Installing security cameras for optimal coverage.
- Calculating the trajectory of projectiles in physics and ballistics.
7. Solving Problems Using Trigonometry
Trigonometry plays a vital role in solving problems related to angles of elevation and depression. By using trigonometric ratios such as sine, cosine, and tangent, you can determine unknown angles or lengths in right-angled triangles.
8. Tips and Tricks for Working with Angles of Elevation and Depression
Here are some useful tips and tricks to remember when dealing with angles of elevation and depression:
- Draw accurate diagrams to visualize the problem.
- Label the known and unknown angles and sides.
- Use appropriate trigonometric ratios based on the given information.
- Pay attention to units of measurement (degrees, radians, etc.).
- Round the final answer to the desired precision.
9. Conclusion
Angles of elevation and depression are essential concepts for understanding heights, distances, and angles in various fields. By mastering these concepts and applying trigonometry, you can solve real-world problems with precision and accuracy. Remember to practice and reinforce your understanding through practical examples and exercises.
10. FAQs
Q1: Can angles of elevation and depression be negative? Angles of elevation and depression are typically measured as positive values. Negative angles may be used in specific contexts where downward angles are represented as negative values.
Q2: What is the relationship between the angle of elevation and the distance to an object? As the distance to an object increases, the angle of elevation decreases, assuming the height of the object remains constant.
Q3: Are angles of elevation and depression only applicable to right-angled triangles? While angles of elevation and depression are commonly associated with right-angled triangles, they can also be applied to other situations involving inclined planes or non-right-angled triangles.
Q4: How can I measure the angle of elevation or depression without specialized equipment? You can estimate angles of elevation and depression using common objects as reference points and your own judgment. However, for accurate measurements, specialized equipment such as theodolites or clinometers is recommended.
Q5: Can angles of elevation and depression be used in 3D modeling and computer graphics? Absolutely! Angles of elevation and depression play a crucial role in creating realistic 3D models and computer-generated imagery (CGI) by accurately simulating the behavior of light and shadows.
